Any classification method uses a set of features or parameters to characterize each object, where these features should be relevant to the task at hand. We consider here methods for supervised classification, meaning that a human expert both has determined into what classes an object may be categorized and also has provided a set of sample objects with known classes. This set of known objects is called the training set because it is used by the classification programs to learn how to classify objects. There are two phases to constructing a classifier. In the training phase, the training set is used to decide how the parameters ought to be weighted and combined in order to separate the various classes of objects. In the application phase, the weights determined in the training set are applied to a set of objects that do not have known classes in order to determine what their classes are likely to be.
If a problem has only a few (two or three) important parameters, then classification is usually an easy problem. For example, with two parameters one can often simply make a scatter-plot of the feature values and can determine graphically how to divide the plane into homogeneous regions where the objects are of the same classes. The classification problem becomes very hard, though, when there are many parameters to consider. Not only is the resulting high-dimensional space difficult to visualize, but there are so many different combinations of parameters that techniques based on exhaustive searches of the parameter space rapidly become computationally infeasible. Practical methods for classification always involve a heuristic approach intended to find a ``good-enough'' solution to the optimization problem.
There are a number of standard classification methods in use. Probably
neural network methods are most widely known. Odewahn et
al. [OSP 
92] applied neural network methods to the
star-galaxy classification problem on digitized photographic plates.
They obtained good results for objects in a limited brightness range.
The biggest advantage of neural network methods is that they are
general: they can handle problems with very many parameters, and they
are able to classify objects well even when the distribution of objects
in the N-dimensional parameter space is very complex. The
disadvantage of neural networks is that they are notoriously slow,
especially in the training phase but also in the application phase.
Another significant disadvantage of neural networks is that it is very
difficult to determine how the net is making its decision.
Consequently, it is hard to determine which of the image features being
used are important and useful for classification and which are
worthless. As I discuss below (§ 3), the choice of
the best features is an important part of developing a good classifier,
and neural nets do not give much help in this process.
A very simple classifier can be based on a nearest-neighbor approach. In this method, one simply finds in the N-dimensional feature space the closest object from the training set to an object being classified. Since the neighbor is nearby, it is likely to be similar to the object being classified and so is likely to be the same class as that object. Nearest neighbor methods have the advantage that they are easy to implement. They can also give quite good results if the features are chosen carefully (and if they are weighted carefully in the computation of the distance.) There are several serious disadvantages of the nearest-neighbor methods. First, they (like the neural networks) do not simplify the distribution of objects in parameter space to a comprehensible set of parameters. Instead, the training set is retained in its entirety as a description of the object distribution. (There are some thinning methods that can be used on the training set, but the result still does not usually constitute a compact description of the object distribution.) The method is also rather slow if the training set has many examples. The most serious shortcoming of nearest neighbor methods is that they are very sensitive to the presence of irrelevant parameters. Adding a single parameter that has a random value for all objects (so that it does not separate the classes) can cause these methods to fail miserably.
Decision tree methods have also been used for star-galaxy classification problems [FWD93, DWF94, Wei94]. In axis-parallel decision tree methods, a binary tree is constructed in which at each node a single parameter is compared to some constant. If the feature value is greater than the threshold, the right branch of the tree is taken; if the value is smaller, the left branch is followed. After a series of these tests, one reaches a leaf node of the tree where all the objects are labeled as belonging to a particular class. These are called axis-parallel trees because they correspond to partitioning the parameter space with a set of hyperplanes that are parallel to all of the feature axes except for the one being tested.
Axis-parallel decision trees are usually much faster in the construction (training) phase than neural network methods, and they also tend to be faster during the application phase. Their disadvantage is that they are not as flexible at modeling parameter space distributions having complex distributions as either neural networks or nearest neighbor methods. In fact, even simple shapes can cause these methods difficulties. For example, consider a simple 2-parameter, 2-class distribution of points with parameters x,y that are all of type 1 when x>y and are of type 2 when x<y (Fig. 2). To classify these objects with an axis-parallel tree, it is necessary to approximate the straight diagonal line that separates the classes with a series of stair-steps. If the density of points is high, very many steps may be required. Consequently, axis-parallel trees tend to be rather elaborate, with many nodes, for realistic problems.
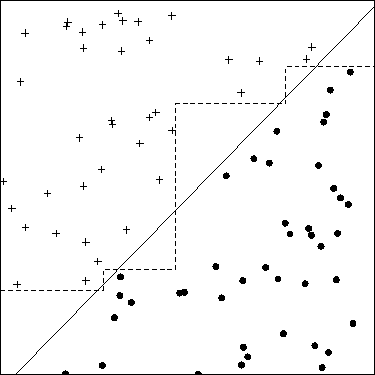
Figure: Sample classification problem with only two features.
Solid line: oblique decision tree. Dashed line:
axis-parallel decision tree. The true dividing line for the simulated
data is the square's diagonal. The oblique decision tree is both
simpler and more accurate than the axis-parallel tree.
Oblique decision trees attempt to overcome the disadvantage of axis-parallel trees by allowing the hyperplanes at each node of the tree to have any orientation in parameter space [HKS93, MKS94]. Mathematically, this means that at each node a linear combination of some or all of the parameters is computed (using a set of feature weights specific to that node) and the sum is compared with a constant. The subsequent branching until a leaf node is reached is just like that used for axis-parallel trees.
Oblique decision trees are considerably more difficult to construct than axis-parallel trees because there are so many more possible planes to consider at each tree node. As a result the training process is slower. However, they are still usually much faster to construct than neural networks. They have one major advantage over all the other methods: they often produce very simple structures that use only a few parameters to classify the objects. It is straightforward through examination of an oblique decision tree to determine which parameters were most important in helping to classify the objects and which were not used.
Most of our work has concentrated on oblique decision trees using the
freely available software OC1
[MKS94], though we have used all the methods mentioned
above. We find that oblique decision trees represent a good compromise
between the demands of computational efficiency, classification accuracy,
and analytical value of the results.
Noise is common in astronomical data. In the presence of noise, classification becomes a statistical estimation problem. Objects should not be classified as either stars or galaxies, but should be assigned probabilities of being in one or the other class.
All of the above methods can be modified to give a probabilistic estimate of class rather than a simple yes or no answer. Neural nets can have an output parameter that represents probability. It is also possible to provide to a neural network (or the other methods, for that matter) the noise in parameters as additional object features. It is hard to know what the neural network actually does with this information, though -- this approach asks the classifier to discover that a particular parameter measures the noise on another parameter. Why should the classifier be burdened with deducing this when we already know what the parameters mean?
The nearest-neighbor method can be generalized to use the K nearest neighbors to an object, which can vote for the object's class. If the vote is not unanimous, it gives an estimate of the uncertainty of the object's majority classification. The same approach can be applied to decision trees. If the search algorithm used to construct the decision tree has a randomized component (which is typical for optimization searches in high dimensional spaces and is in fact the case for OC1), one can construct a number of different decision trees and let them vote on an object's class.
For decision trees, it is also possible to use known noise estimates for the parameters to determine at each node the probability that an object belongs on the left branch or the right branch. These probabilities, multiplied down to the leaf nodes and summed over all the leaves belonging to a particular class, give a probability that an object belongs that class. We are just beginning to explore this approach, which has great intuitive appeal and appears to be a promising avenue for further work.