Inhomogeneous data sets can make developing a classifier devilishly difficult. In the Guide Star Catalog II (GSC-II) star/galaxy classification problem, for example, there is a considerable variation in the characteristics of images from different photographic plates. The sky brightness and atmospheric ``seeing'' (which determines the stellar image size) change with time. The telescope optical characteristics also cause a slow variation in these parameters from the center to the edges of the plates. The atmosphere causes the images of objects photographed directly overhead (at the zenith) to differ from images of the same objects photographed near the horizon. Finally, the photographic plates themselves do not all respond identically when exposed to light. All of these factors combine to make the image features of identical objects appear to change from one plate to another.
Almost all large-scale surveys have similar problems. The Sloan Digital Sky Survey does not suffer plate emulsion variations, but it will have seeing, sky, and zenith-angle variations.
The straightforward solution to this problem is to generate many training sets to cover all the possible variations in object parameters. That is almost never a viable approach, however. For the GSC-II project, we have many thousands of photographic plates. Both the human expense of generating training sets and the computational expense of retraining the classifier on each plate are prohibitive.
A better approach is to find image parameters that are independent of the plate-to-plate variations. This section describes a new approach to generating robust parameters for classification. This approach appears to solve our problems for the GSC-II; it is a very general technique that will be applicable to many other problems as well.
It is not terribly difficult to find image parameters that separate
stars and galaxies for a single GSC-II plate. Figure 3(a)
shows a scatter-plot of the total density
(summed over all pixels in
the object) versus the peak density (brightest pixel) for objects
from one plate.
Stars and
galaxies for this training set were identified using the
deep CCD catalog of Postman [PLG 
96].
Stars are (mainly) well-separated from galaxies: stars
have sharper images and so have brighter peak density values for a
given total density. The distribution is non-linear as a result of
the non-linear response of the photographic plate to light, but
otherwise a reasonably simple and accurate classifier can be
constructed using only these two parameters.
The problem gets very messy when one compares objects from different plates. Figure 3(b) shows the same plot with objects from five different plates. The well-defined distributions for individual plates can be discerned here, but it would be practically impossible to develop an accurate classifier based on these parameters.
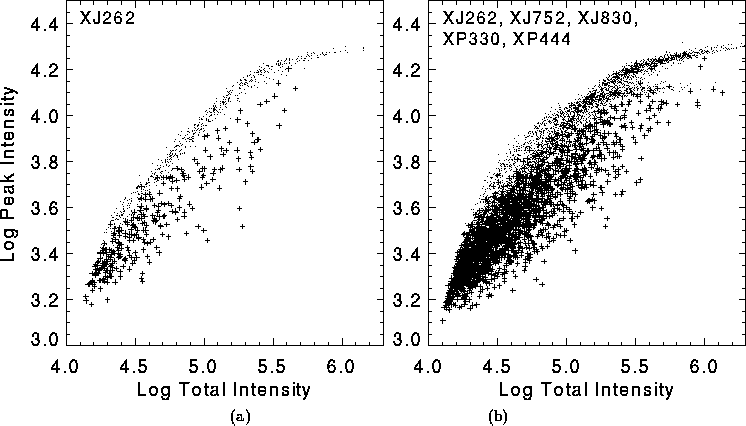
Figure: Total density versus peak density for stars (dots)
and galaxies (plusses)
measured on GSC-II photographic plates. (a) The distribution for a single
plate (XJ262) is well-defined and could be used for classification. (b) The
distribution for five plates differs for different plates and so a classifier
for all plates could not be constructed from these parameters.
We are currently using what appears to be a new approach for scaling these parameters so that they are plate-independent. The idea for this scaling grew from some methods used in robust statistics. A standard ``trick'' in robust statistics is to use not the value of a parameter but its rank. For example, the Spearman rank-order correlation coefficient can be used to test for a correlation between two variables using not the actual values of the variables but their ranks.
The advantages of ranks in statistical applications are well-known: by using ranks, we are able to construct statistical tests that do not rely on the probability distribution of the variables. The ranks are by definition uniformly distributed. Similarly, using ranks for classification allow us to use parameters such as the total and peak intensities even though their detailed distributions vary from plate to plate.
In the current application, we proceed as follows. We compute the ``raw'' feature values for all objects on a plate (or on a portion of the plate if there are variations within the plate.) We then sort the raw values of each parameter and determine the rank of each raw value within the sorted list. These ranks are scaled to be in the range zero to one. Thus each of the raw features is transformed into a corresponding rank feature.
Note that the ranks are computed separately for objects from each plate. Once converted to ranks, the features for all objects can be combined and a single classifier can be used for objects from different plates.
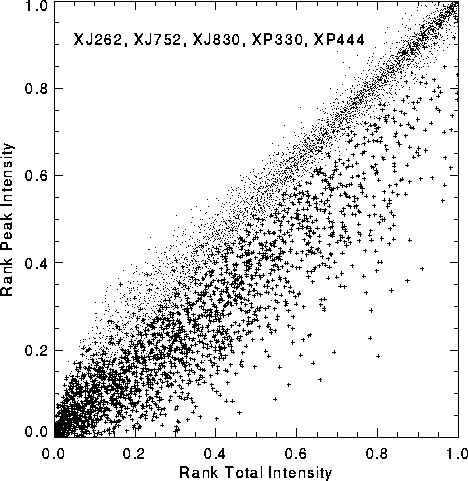
Figure: Distribution of total density versus peak density
for objects from Fig. 2(b) after transformation
using ranks. Stars and galaxies from different photographic
plates separate very well. An accurate classifier can be constructed
based on these rank parameters.
Figure 4 shows the distribution of the total density rank versus the peak density rank for the same five plates shown in Figure 3(b). Using the rank transformation results in excellent separation between stars and galaxies. Transforming these parameters using their ranks has three significant benefits for our classifier. (1) The distributions become much more similar on different plates. (2) The distribution of objects with feature values becomes uniform, so for example there are equal number of objects in the intervals (0,0.1) and (0.9,1). That makes separating objects in feature space easier. (3) The line separating the stars from galaxies becomes nearly perfectly linear, which makes the decision tree classifiers even more effective than they would be for the untransformed features.
A single decision tree classifier with an accuracy of 91.5% on all five plates can be constructed using only these two parameters. Most of the classification errors are faint, noisy objects. When additional features are included, we are able to construct a classifier with an accuracy of 95-96% for all objects and 98-99% for moderately bright objects (see Fig. 5.) We apply the rank transformation to most of the additional parameters. The complete details of our classifier and the features we are using will be reported elsewhere.
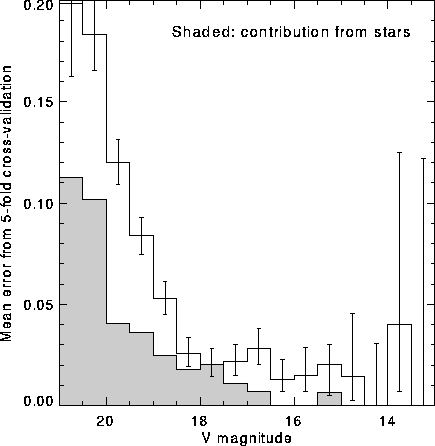
Figure: Error rate as a function of object brightness for
oblique decision tree based on parameters transformed using ranks.
All objects in the training set shown in Figures 3 and 4 are
included. Excellent accuracy is achieved for brighter objects,
and even for faint objects the accuracy is good.
This method was developed only recently, and some details are still being worked out. What is the best way to store the rank transformation so that small object lists (e.g., from small images extracted from the plate) can be classified? How can we best adapt this method to cases where the population of objects changes substantially from one data set to another? For example, in the plane of the Milky Way, the sky images are densely crowded with many stars; galaxies are rare or non-existent. Looking straight up out of the plane of our galaxy, stars are scattered much more sparsely across the sky and a larger fraction of the objects are galaxies. It may be necessary to have independent training sets for the two extremes and to somehow interpolate between them for intermediate regions of the sky.
Despite the uncertainty about how some details should be properly handled, it is clear that this new method is a powerful tool for converting parameters to a more useful form that in most cases leads to simpler and more accurate classifiers.