The FIRST log N - log S

 

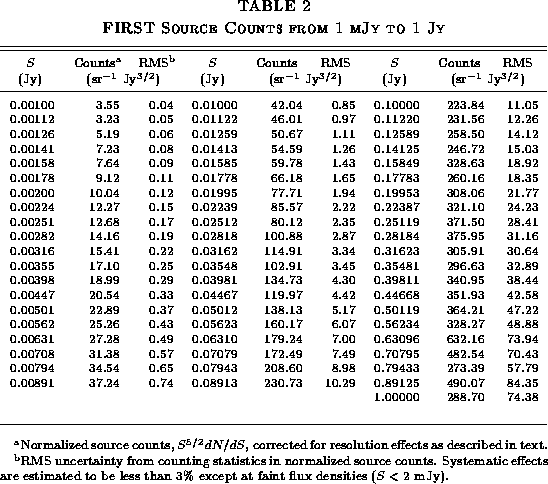
The number of sources as a function of flux density is of interest both as a measure of the evolution of cosmic radio sources and also as a powerful test of the completeness and accuracy of the FIRST radio catalog. We have computed the dN/dS distribution of FIRST sources from our catalog for comparison with previous observations of 1.4 GHz source counts.

A number of corrections must be applied to the raw histogram of source counts versus integrated flux density in order to derive the true dN/dS. We must first account for the varying sensitivity of the survey. Each source in the histogram is assigned a weight equal to the inverse of the area over which the source could have been detected ([Katgert et al. 1973]). We compute this area from the coverage map by summing the areas of all pixels with rms noise for a source with fitted peak flux density before CLEAN bias correction. Note that sources with  mJy/beam can be detected anywhere in the survey area, so the effective area covered is constant above that peak flux density threshold. However, sources with large integrated flux densities can still have low peak flux densities, so the dN/dS histogram is affected by the areal coverage at integrated flux densities well above this threshold.

The next step is to combine close groups of sources, which usually are not independent objects but rather are components of a single object. To be consistent with previous studies ([Oosterbaan 1978], [Windhorst et al. 1985]), we have merged sources that fall within 50" of their nearest neighbors. Nearly 30% of the FIRST catalog entries fall in such groups, which reduces the number of sources in the dN/dS histogram by %.

The appropriate weighting for merged sources is somewhat complicated. Since the sources in a pair have different fluxes, they can have different associated survey areas over which the sources could have been detected. Suppose we have two sources with integrated flux densities and detection areas . In area , both components of this pair are detected; in area only the brighter component (source 2) would be detected; and in the remaining survey area neither component would be detected. Consequently, for this pair we not only have to add a contribution to the flux bin , but we also have to subtract a contribution from bin to correct for source pairs where was not detected. The weights for the pair are in bin and in bin . For groups with more than 2 sources, a contribution is subtracted from several bins representing partial sums of the brighter source flux densities and added to the bin that includes the sum of the integrated flux densities of all components.

Another complication introduced by merging sources is that some merged sources are not components of a single objects but are independent objects that happen to fall close together in the sky. The FIRST catalog has  sources/ , so % of the sources are expected to have a random neighbor within 50". Most of the randomly merged sources fall at the faint end of the flux distribution, since most sources in the catalog are faint. If the true source distribution is f(S) = dN/dS, then the observed distribution after random mergers is

The function is the flux distribution of randomly merged groups containing n sources:

where

is the distribution of single (unmerged) sources. Here is the mean number of sources per merging area A:

As long as (as is the case for the FIRST catalog with a 50" merging radius), a simple way to solve for f(S) given is to use the method of successive substitutions, starting with and iterating

Correcting the FIRST dN/dS distribution using this approach leads to an increase of % in the source counts between 1 and 2 mJy, with the correction declining to a negligible level above  mJy.

  
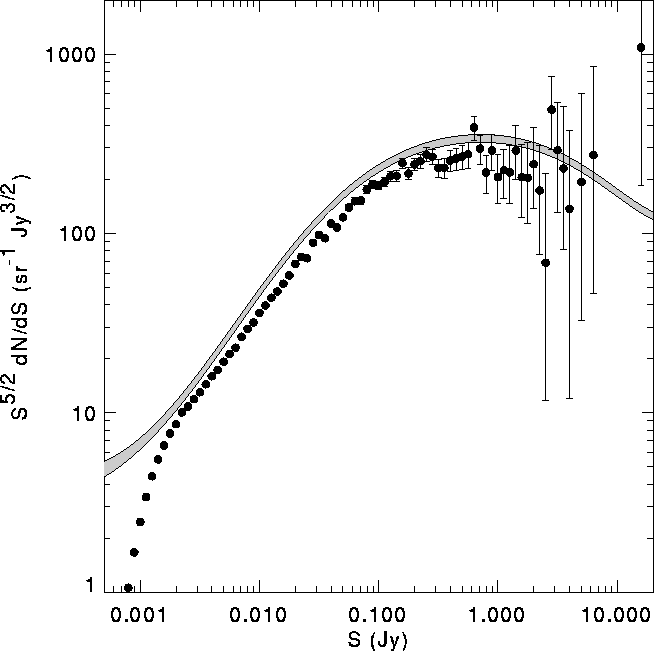
Figure: Flux density distribution of FIRST catalog sources before correction for resolution effects. The differential FIRST source counts, normalized to the distribution expected for a non-evolving population in flat space, is plotted versus the integrated flux density. Sources closer than 50" are assumed to be components of a single object and have been merged. Flux densities have been corrected for CLEAN bias, and a small correction has been applied to account for the random merging of independent sources. The shaded line shows the dN/dS distribution determined by Windhorst et al. (1984, 1985, 1990).

The resulting merged dN/dS distribution is compared with the distribution derived by Windhorst ([Windhorst 1984, Windhorst et al. 1985, Windhorst et al. 1990]) in Figure 9. The shape of our distribution is very similar to Windhorst's observations, but the FIRST counts are too low by %. This normalization difference is due to the fraction of sources that are partially resolved by our B-configuration observations and so have integrated flux densities in the FIRST catalog that are too small. We can correct the dN/dS distribution for this resolution effect using the lost flux versus size distribution determined from comparison to the NVSS catalog (Fig. 7) along with the source size distribution. We show the dN/dS distribution before correction for resolution effects mainly to demonstrate the amplitude of these effects, which are modest and can be neglected for many purposes. In cases such as computing dN/dS where a correction must be applied, the corrections required are not dramatic.

Assume that the ratio R of the observed brightness of a source to its true brightness is a function only of the source's major axis FWHM . We model the empirical shown in Fig. 7 using the simple analytical function

 

Using this function, we have computed the expected distribution of R for FIRST catalog sources by taking the size distribution of NVSS sources brighter than 20 mJy (fainter sources have very noisy sizes) and computing from it the distribution of R values. When normalized by the number of sources, this gives the probability that a source will have a given value of R. The results are shown in Figure 10.

  
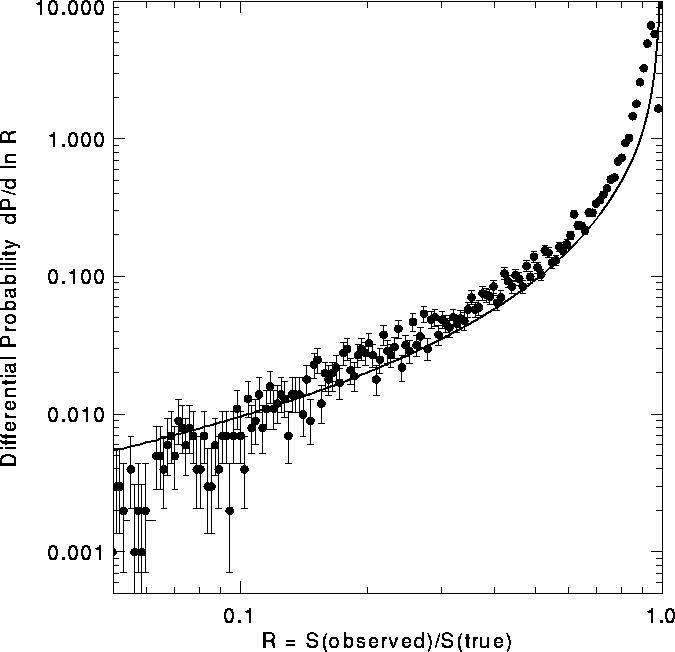
Figure: Distribution of ratio of observed flux density to true flux density for FIRST sources expected based on the NVSS size distribution and the FIRST/NVSS flux ratios (Fig. 7). The line shows the prediction based on the Windhorst et al. (1990) size distribution, which is in excellent agreement with the data. The excess of sources over the model near R=1 is the result of noisy size estimates for sources that are small compared with the 45" NVSS beam.

The source size distribution (and so the R distribution) is known to vary with the source flux density ([Oort 1988, Windhorst et al. 1990]). [Windhorst et al. 1990] propose two simple functions describing the size distribution. The integral size distribution is

 

where the median size is

with S in mJy. The line in Figure 10 is the distribution derived by combining this size distribution with the observed NVSS flux density distribution, accounting for the  mJy flux cut applied to the data. The model ratio distribution is practically identical to the observations, which gives us confidence that the Windhorst distribution can be applied to our data.

The effects of resolving out flux on dN/dS are most conveniently computed using the source count distribution in . A flux ratio R corresponds to a difference between the true and observed log flux values . The observed dN/dz distribution is a convolution of the true distribution g(z) with the resolution function P(Q):

Deriving g(z) from is a deconvolution problem if the size distribution does not depend on the source flux density. In our case, the size distribution does depend on flux: P(Q|S) is the probability of a log flux ratio Q for a source with true integrated flux density S. Then the equation we must solve is

This is not simply a convolution, but it is still an inverse problem solvable by techniques similar to deconvolution.

We have used the Richardson-Lucy method ([Lucy 1974]) to perform the resolution correction for the merged FIRST dN/dS. The Richardson-Lucy iteration finds the maximum likelihood solution to the deconvolution problem in the presence of Poisson noise in the data ([Shepp & Vardi 1982]). Since the noise in our problem is mainly due to counting statistics (though it has been slightly modified by the weighting and merging schemes described above), this method is a good choice for the deconvolution. Forty iterations of the Lucy method were used; it converges rapidly because P(Q|S) is strongly peaked near Q=0.

The ``point-spread function'' P(Q|S) was computed from the [Windhorst et al. 1990] size distribution (Eq. 8) and the empirical flux loss function (Eq. 7). We have included in P(Q|S) a Gaussian noise of 0.2 mJy/beam in the peak flux densities, which also acts to blur the true dN/dS. Note that the size distribution gets cut off at a flux-dependent maximum size where the peak flux density drops below the 1 mJy/beam survey threshold.

  
Figure: The FIRST source counts from Fig. 9 corrected to account for the loss of flux from some sources due to the resolution of extended objects in the VLA B-configuration (Fig. 10). The corrected distribution is in excellent agreement with the Windhorst distribution (shaded). The scatter at bright flux densities is the result of mild noise amplification in the deconvolution. Over the flux density range 2-30 mJy this is the most accurate determination ever made of the radio distribution.

Figure 11 shows the FIRST dN/dS corrected for resolution effects. The corresponding counts are given in Table 2. It is in excellent agreement with previous determinations ([Windhorst et al. 1985, Windhorst et al. 1990]) over 4 orders of magnitude in integrated flux. Over the flux density range 2-30 mJy this is the most accurate determination ever made of the radio distribution. The statistical errors are very small, and we estimate that the systematic errors (from flux scale errors, uncertainties in the resolution correction, etc.) to be less than 3% except at faint flux densities. The roll-off at flux densities less than  mJy is due to the low peak flux densities of many faint, extended sources, which make them undetectable in our survey. This is a useful indication of the incompleteness of the survey at the faint limit.