5 Optical Identification of FIRST Radio Sources

The primary condition for assigning an optical counterpart to a radio source has traditionally been positional coincidence; while other factors can enhance or detract from the probability that the association is correct, these are generally second-order effects. If the positional accuracies for both the radio and optical catalogs are very high, positional coincidence alone can afford a high degree of confidence. In BWH, we calculated the expected error rate for associations between the APM and several hypothetical VLA radio surveys with differing angular resolutions. The reliability of associations based on positional coincidence were presented as a function of optical source density on the sky, and as a function of apparent V magnitude at the North Galactic Pole. The results demonstrated the strong dependence of both reliability and completeness on the angular resolution of the radio survey.

In reality, the actual error rate in radio/optical associations is a complex problem depending on the details of the relative astrometric accuracy of the two data sets, the optical morphology of candidate objects, and radio source morphology. In this section we quantify empirically the reliability of associations between FIRST radio sources and optical counterparts on the POSS-I plates as measured by the APM.

1 Background Rates Using Closest Matches

In our analysis of the FIRST-APM match rate, we retain only the closest optical match to each radio source and vice versa. While the optical catalog we present below includes all matches out to $20^{\prime\prime}$, not just the closest one, using only the closest matches when describing the identification statistics makes understanding the background and true match rates easier. We want to know the number of radio sources that have optical counterparts, but we want to avoid double-counting (e.g., a particular optical object may be the closest counterpart for two different radio sources.) Also, neither catalog can have pairs of sources with separations of less than a few arcseconds, which means that there is effectively a ``hole'' in the catalog around each radio or optical source. This makes it very difficult to calculate chance coincidence rates, since true matches suppress additional false matches in a complicated manner.

We can avoid both of these problems by using only the closest matches. This also modifies the chance background rate, since once a source has a counterpart there can be no additional counterparts at wider separations. This effect is straightforward to understand and incorporate into the background computation: the area being searched for new matches at a given radius is contributed only by FIRST sources that do not already have a closer optical counterpart. Another complication when using closest matches is that the matching circles for close pairs of radio sources can overlap. An optical source that falls in the overlap region between two radio sources can only be assigned as the counterpart to one of them. This is also a mathematically tractable problem. Both effects are treated as a reduction in the effective sky area that is searched as a function of matching separation.

When both of these effects are taken into account, it is possible to predict the number of chance (false) coincidences as a function of the radio-optical separation. A simple model for this prediction that assumes a uniform, random distribution of optical sources on the sky predicts more coincidences at large separations than are actually seen, owing to the variation in optical source density $\rho_{opt}$ on the sky. In the presence of a varying optical source density, radio sources that remain unmatched at large separations are more likely to be found in low-density areas of the sky; consequently, the effective mean optical source density decreases as the separation increases. If the variation $\delta\rho_{opt}/\rho_{opt}$ is not too large, this can also be modeled fairly simply. For an ensemble of $N$ radio sources, the effective background source density is

$$\rho_{eff}(r) = \bar{\rho}_{opt} - \sigma_{opt}^2 \left( \sum_i A_i(r) \phi_i(r) \over \sum_i \phi_i(r)\right) \quad,$$ (6)

where $\bar{\rho}_{opt}$ is the mean source density, $\sigma_{opt}$ is the rms variation in the density, $A_i(r)$ is the area already searched for source $i$, and $\phi_i(r)$ is the angular part of the matching circle being searched for source $i$. For an isolated FIRST source with no nearby neighbors (so there are no overlapping error circles) and an optical match at radius $r_0$, we have

$$\phi_i = 2\pi \quad , \quad r < r_0 \quad$$ (7)

$$= 0 \quad , \quad r > r_0 \quad ,$$ (8)

and

$$A_i = \pi r^2 \quad , \quad r < r_0 \quad$$ (9)

$$= \pi r_0^2 \quad , \quad r > r_0 \quad .$$ (10)

For ``gregarious'' FIRST sources in close groups, the matching circles overlap. Then $\phi_i$ will include only the portion of the error circle at $r$ that would not be assigned to another FIRST source, so that in general $\phi_i \le 2\pi$.

Our background model, then, has two parameters: the mean source density $\bar{\rho}_{opt}$ and the variance in the density $\sigma_{opt}^2$. Values for these quantities were estimated from a spurious match catalog generated by offsetting the coordinates of the radio sources by $5^{\prime}$ to the south. We use this procedure instead of simply adopting the match rate between, say, 10" and 20" around the real source positions in order to minimize any enhancement in the false rate resulting from the presence of real radio-optical associations at large separations. Such associations result both from optical counterparts to multiple-component FIRST objects (where the optical position need not match any one of the cataloged FIRST components closely) and clustering of galaxies around FIRST objects (which will produce an uncharacteristically high optical source surface densities in the vicinity of the radio sources.) The parameters for the background due to various types of APM objects are given in Table 1.

2 Match Results

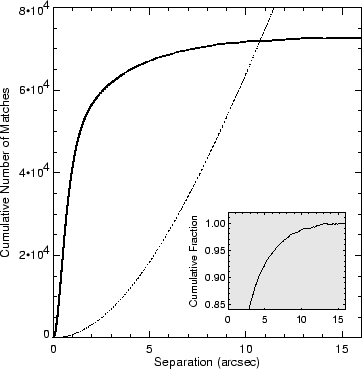
In Figure 8, we display the result of matching all 382,892 radio sources in our catalog to the astrometrically corrected APM catalog. The plot shows the cumulative excess of matched sources over the background of chance coincidences as a function of the offset between the radio and optical positions. We estimate that 98% of the APM sources within 1" of a FIRST source are physically associated with the radio source; 42,400 sources meet this criterion. Even out to 2", 94.5% of the 59,700 associations are real. Figure 8 indicates that some real matches occur out to $>10$" although the reliability decreases steadily as the separation increases. Integrating under the curve of Figure 8 out to 4" implies 61,800 real associations (16% of all radio catalog entries). Inside the 1" radius, 16% of the optical counterparts are classified as stellar on both plates, while 41% are classified as non-stellar on both plates; in the remaining cases, the classifiers disagree or the object is only detected on one plate. Note that, at faint magnitudes, classification becomes difficult owing to the limited number of pixels above threshold; in addition, active nuclei can make a galaxy appear stellar in the blue band, and the bulges of faint ellipticals and SOs are generally unresolved. Thus, galaxies are increasingly classified as stellar as the plate limit is approached.

Figure 8: The cumulative number of FIRST-APM matches as a function of separation. Only the closest APM object to each FIRST source is included; both isolated and ``gregarious'' FIRST sources (those with near neighbors) are included. The background coincidence rate (dotted line) has been subtracted. The inset shows the cumulative fraction of sources as a function of radius with an expanded scale. The vast majority of matches within $2^{\prime \prime }$ are clearly true identifications; a few true identifications are found out to $>10^{\prime \prime }$ separations. A total of $\sim 73,000$ FIRST sources have optical counterparts in the APM catalog.

In Table 3 we tabulate the completeness and reliability of objects that are only detected on a single red or blue plate. These have been estimated by shifting the radio positions by 3 arcmin in declination and running the matching analysis in an identical manner on this shifted dataset. This shows that 92.7% of the blue-only matches within 1" are real, and 97.5% of the red-only matches within 1" are real matches. This is a lower limit on whether these single band detections are real objects since we expect some of the the chance associations to be real celestial objects.

The matching results are more complicated to analyze when we take into account the complex radio sources that get broken into two or more components in the FIRST catalog. We call these ``gregarious'' sources (as distinguished from isolated sources) because they are found in clumps on the sky. Note that some gregarious sources are simply the chance superposition of two unrelated radio emitters at different distances; nonetheless, from our vantage point, they are gregarious, and confuse the matching statistics in a manner similar to that of the real multi-component objects. We define the sociological boundary between gregarious and isolated at $60^{\prime \prime }$; i.e., any source with no other catalog entry within a radius of $60^{\prime \prime }$ is classified as isolated, and all other sources are labeled gregarious. Such a fixed boundary is arbitrary, and, indeed, a small number of very extended objects will be incorrectly classified as isolated; we discuss this matter further in § 5.

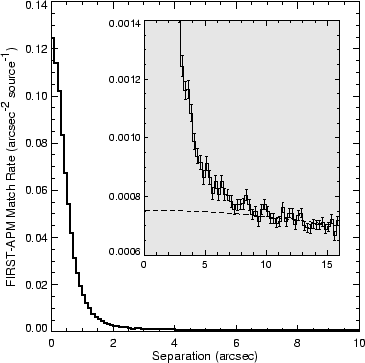
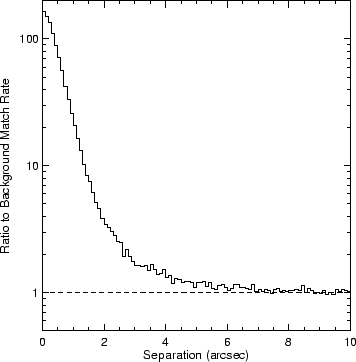
In Figure 9, we display the number of isolated matched sources as a function of the offset between the radio and optical positions in 0.1" bins, normalized by the annular area of each bin. Figure 10 displays the ratio of the number of matches to the predicted false rate as a function of separation.

Figure 9: A histogram of the number of matches as a function of separation between the FIRST and APM positions. Only the closest APM match to each FIRST source is included, and only isolated FIRST sources have been included to avoid the ambiguities in the background computation for multiple-component FIRST matches (see Fig. 13.) The histogram has been normalized by the product of the area of each annular bin and the number of FIRST sources, so it gives the mean number of APM matches per unit area for each FIRST source. The background rate of coincidental matches is shown in more detail in the inset (error bars are $1\sigma$ and the dashed line shows the expected chance coincidence rate.)

Figure 10: The ratio of the number of APM-FIRST matches to the expected number of coincidental matches as a function of separation. As for Fig. 9, only the closest APM matches to isolated FIRST sources are included. This function shows the effect of increasing the matching radius between the catalogs. At a separation of $\sim 2.5^{\prime \prime }$, the background rate per unit area is approximately equal to the true match rate, so a small increase in the matching circle size leads to about equal numbers of true and false matches being included. Within $2\arcsec$ the vast majority of the matches (98%) are real associations; when non-isolated FIRST sources are included, this fraction declines to 95%.

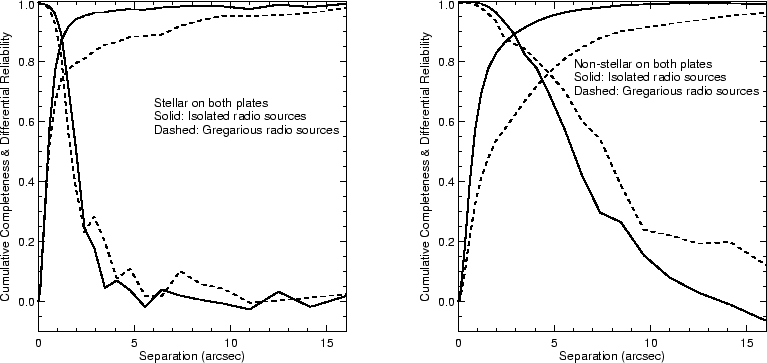
Both the background rate and the typical angular separation between FIRST and APM positions depend strongly on the optical classification. Figure 11 shows the distribution of separations for sources classified as stellar on both plates or non-stellar on both plates. The FIRST-APM positions typically differ by more for galaxies, which have less well-determined optical positions. However, it is easier to identify galaxies confidently as FIRST counterparts because the background rate for galaxies is four times smaller than for stars (see Table 1).

Figure 11: The match rate as a function of separation for (a) APM objects classified as stellar on both the POSS-I plates and (b) APM objects classified as non-stellar on both plates. As for Fig. 9, only the closest APM matches to isolated FIRST sources are included, and the insets show the counts to larger radii with a much expanded scale. Galaxies are less concentrated to small separations than stars (mainly because the optical positions are less well-determined), but the background rate for galaxies is four times smaller than that for stars, which makes matches to galaxies reliable to larger radii than those for stars (see Fig. 12).

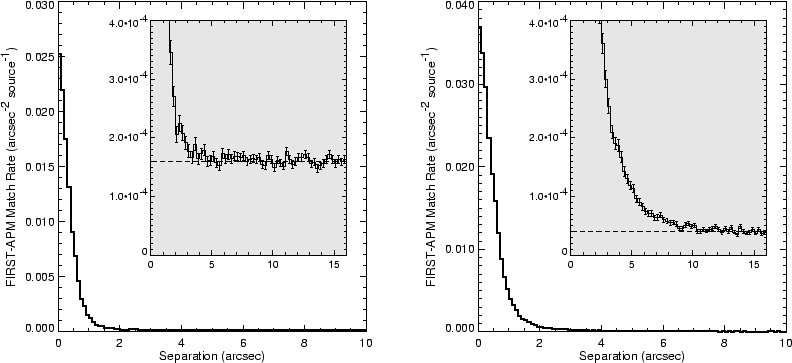We quantify this effect by calculating the angular radius which contains 90% of the real associations as well as the percentage of false matches within the same radius. For example, these numbers are 4.2" and 17% for the distribution of all FIRST/APM sources as shown in Figure 8. If we restrict the match to APM objects that are classified as galaxies on both plates (Fig. 11b), the values are $4.0^{\prime\prime}$ and 2.7%. The 90% radius is quite similar to that for all associations, since galaxies constitute the majority of all identifications; however, the reliability for galaxies is much higher because the background rate for galaxies is smaller (Fig. 11). By comparison, if we restrict ourselves to APM sources that are stellar on both POSS plates (Fig. 11a), the 90% radius and error rate are $1.7^{\prime\prime}$ and 6%. The smaller footprint of stars on the POSS-I leads to more accurate optical positions (hence the smaller 90% radius). These and other cases are summarized in Table 2 and in Figure 12, which displays the completeness and reliability of matches as a function of separation.

Figure 12: Completeness and reliability as a function of separation for (a) objects classified as stellar on both APM plates and (b) objects classified as non-stellar on both plates. The completeness rises almost monotonically from zero to one as the separation increases (the small deviations from monotonicity are due to the background subtraction). The differential reliability, which measures the probability that sources at a given separation are true associations rather than chance coincidences, declines toward larger separations. The solid lines show the rates for isolated FIRST sources, while the dashed lines are for gregarious FIRST sources. Stellar matches to isolated sources are very closely concentrated toward small separations, and few stellar matches beyond a few arcseconds are real. On the other hand, because the background rate for non-stellar matches is much smaller (see Fig. 11), matches with galaxies are reliable to much larger radii.

3 The Effects of Radio Morphology

The statistical agreement between FIRST and APM positions is also affected by the morphology of FIRST sources. If we restrict the FIRST sample to point-like radio sources (but include all APM sources), the 90% association radius is 2.0" with a false rate of 5%. Limiting the discussion to sources that are point-like in both the radio and the optical results in 90% of the matches within 1.1" with a 2.4% false rate.

Figure 13: The normalized histogram of separations for isolated FIRST sources (with no other cataloged FIRST objects within $60^{\prime \prime }$) and ``gregarious'' FIRST sources (which do have neighbors in the catalog.) The background coincidence rate has been subtracted. Clearly most of the matches at large separations are attributable to the multiple-component gregarious sources, where the position of the optical counterpart is not as tightly coupled to the FIRST radio position as it is for isolated sources. Developing a matching strategy for gregarious FIRST sources and determining the chance coincidence rate is a difficult problem which we begin addressing in § 5.4.

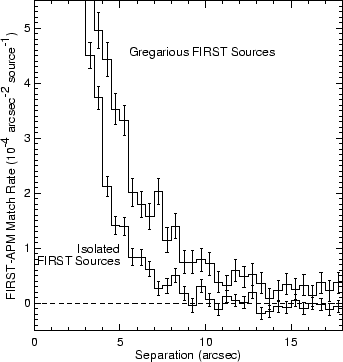Figure 13 compares the histogram of separations for isolated sources with that for the gregarious sources. It can be seen that gregarious sources contribute most of the matches at large separations; indeed, they show evidence for a statistically significant excess of matches even beyond $15^{\prime\prime}$. Many of the gregarious FIRST sources are components of classical double radio sources, which may have no radio component at the center of the double. Consequently the optical counterpart will typically be $\sim1/2$ the double separation from each component. We now begin to explore counterpart identification strategies for such sources.

4 Optical Counterparts to Double Radio Sources

The wide variety of radio source morphologies (not to mention the extent to which their appearance depends on the resolution of the survey) makes it difficult to design a robust algorithm that predicts the locations of the optical counterparts to multiple-component sources. We present here an empirical approach to the problem for the simplest class of such sources - isolated doubles.

Figure 14: The distribution of angular separations of all isolated pairs of FIRST sources (no third component within $120^{\prime \prime }$). The minimum separation of $3^{\prime \prime }$ is set by the resolution of the FIRST images and our detection algorithm; the fall-off beyond $10^{\prime \prime }$ arises from a variety of effects (see text). The dashed line represents an estimate of the chance coincidence rate. At a separation of $40^{\prime \prime }$, approximately half the doubles are physically associated and half are chance superpositions of unrelated sources

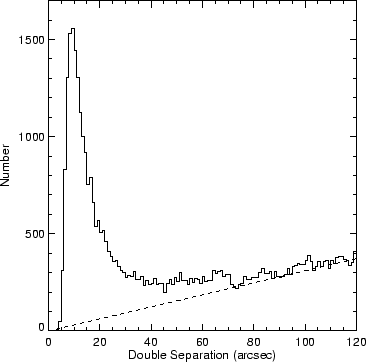Figure 14 displays the distribution of $\sim 45,000$ isolated pairs of FIRST sources as a function of their separation. The minimum value of $3^{\prime \prime }$ is imposed by the source detection algorithm (WBGH). The fall-off in the number of detected doubles beyond $\sim 10^{\prime\prime}$ reflects a number of factors: 1) the $5^{\prime\prime}$ survey beam resolves out very extended features and will therefore not detect sources on the largest scales, 2) the exclusion of triples and other multiple component sources from this subsample will preferentially remove extended sources on larger scales, and 3) there is a real decline in the number of large angular-diameter objects. For comparison with the APM catalog, we have selected objects with separations in the range $8^{\prime\prime}<d< 30^{\prime\prime}$.

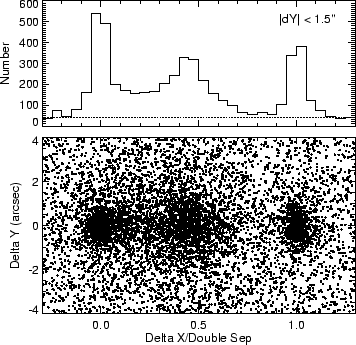
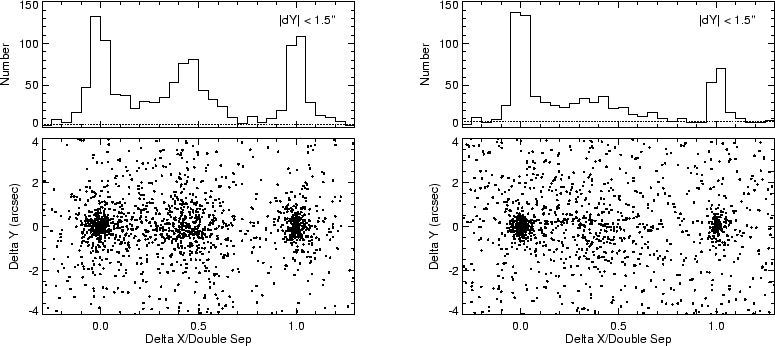
The lower portion of Figure 15 displays the distribution of optical objects in the vicinity of the 21,579 pairs of radio sources meeting this criterion. The x-axis for each pair is defined by the line joining the centroids of the two objects; the scale is normalized to the separation, with the origin chosen as the brighter of the two components. The upper panel shows a histogram for all optical objects within $1.5^{\prime \prime }$ of the line joining to two components; the expected false rate from a uniform distribution of sources with the same mean surface density as the FIRST survey is shown as the dashed line. Several features of the distribution are immediately apparent. There is a large concentration of optical objects coincident with the brighter of the two radio components, suggesting a core-jet morphology. A roughly equal number of identifications is found approximately half way between the two components with a slight bias in the direction of the brighter lobe; the broader spread in the y-direction for these counterparts reflects in part the bending of radio lobes as a consequence of their interaction with the intergalactic medium (e.g., Blanton et al. 2000, 2001). Finally, a much smaller fraction of the identifications is coincident with the weaker of the two lobes. The overall identification rate derived from integrating the upper curve and subtracting the background rate is $\sim19$%, similar to that for the radio sample as a whole.

Figure 15: The distribution of the 8220 optical objects in the vicinity of the 21,579 isolated doubles with separations between $8^{\prime \prime }$ and $30^{\prime \prime }$. The axes are defined such that the line joining the two component centroids is the x-axis and the normal to this line is the y-axis. Distances along the x-axis are normalized to the component separation with the origin defined to coincide with the brighter of the two components; the y-axis is in arcseconds. The lower panel shows the distribution of all optical objects, while the upper panel displays a histogram of the 5348 objects falling within $\vert y\vert<1.5^{\prime \prime }$. The false rate is shown as the horizontal dashed line.

Figure 16: Using the format of Fig. 15, we display the results for optical counterparts to radio doubles divided between (a) the 1492 objects classified as galaxies on both plates and (b) those 1278 objects classified as stellar on both plates.

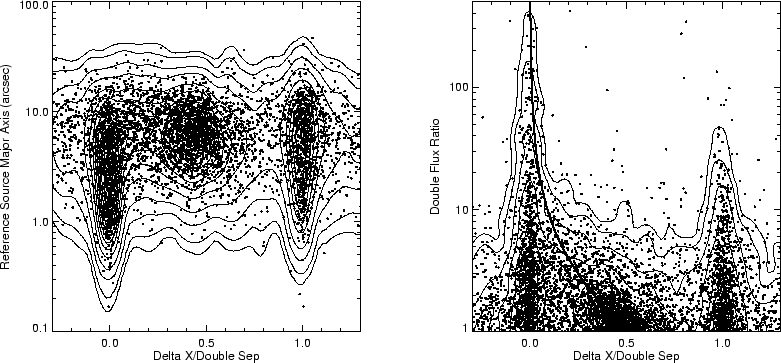
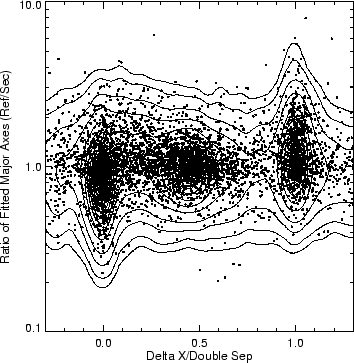
Dividing the optical counterparts by morphological class yields additional interesting results. The objects classified as galaxies on both plates (Figure 16a) produce the most counterparts midway between the components, while the stellar objects are predominantly associated with the brighter radio component (Figure 16b). Figure 17 shows that many of these core components are small in size (panel a) and are much brighter (panel b) than the other component: the median flux ratio for sources where the optical counterpart matches the brighter radio component is 3.0, while the median for the central-component matches is 1.4. When the brighter of the radio components identifies the optical counterpart, it also tends to be the smaller of the two components (panel c). Likewise, for cases in which the dimmer source has the optical counterpart, it tends to be smaller. In contrast, the sources with identifications that lie between the two radio lobes have very narrow ranges of flux density and size ratios near unity, and are virtually all resolved.

Figure 17: (a) The angular size of the brighter radio component for the 5348 doubles that have optical counterparts within $1.5^{\prime \prime }$ of the line joining them, versus the distance along that line (normalized to the double separation as in Fig. 15). Contour lines illustrate the density of points in various parts of the diagram at levels of 0.01, 0.02, 0.05, 0.1, 0.2, 0.3, ..., 0.9 of the peak. A source is clearly resolved in the FIRST survey if it has an angular size greater than 2.5- $3^{\prime \prime }$. (A total of 125 objects with deconvolved sizes of $0.0^{\prime \prime }$ are omitted from the plot; 54 fall near $dx=0$, with 51 near $dx=1$ and only 12 lying between the components.) The brighter of the two components (which defines the x-origin) is more often point-like. (b) The ratio of the flux densities of the radio doubles with counterparts as a function of distance along the line joining the two components. In cases where the optical counterparts coincide with one component or the other, the components tend to have very unequal flux densities, whereas for cases when the optical counterpart is between the two components, the doubles are of nearly equal flux density. The thick line indicates the flux-weighted centroid of the source.

Figure 17: (c) The ratio of the fitted major axes of the doubles with counterparts as a function of distance along the line joining the components, defined as the size of the brighter component over the size of the dimmer one. When the optical counterpart coincides with one component or the other, the size of that component is smaller, whereas when the counterpart is found between the two components, they tend to be of equal size.

Using these trends in radio source component flux density and size ratios, total extents, and optical morphology (in addition to magnitude and color, perhaps) it would be possible to develop a reasonably reliable identification algorithm for double and multiple FIRST sources, although we regard such an effort as beyond the scope of this paper. What is clear from the foregoing analysis is that, since the identification rate for complex sources is similar to that for single-component objects, the effect on the final fraction of radio emitters identifiable at the POSS-I plate limit simply scales with the number of radio components removed from consideration as a consequence of their association with another catalog entry. Using an algorithm that assigns a probability to component associations based on flux density and separation, we find that, for separations up to $120^{\prime \prime }$ there are 32,312 doubles, 12,802 triples, and 5,716 groups of four or more sources with a probability of real association $>90\%$. This reduces our catalog to $\sim 306,000$ discrete radio emitters and yields an overall identified fraction at the POSS-I limit of $\sim24$%.